 |
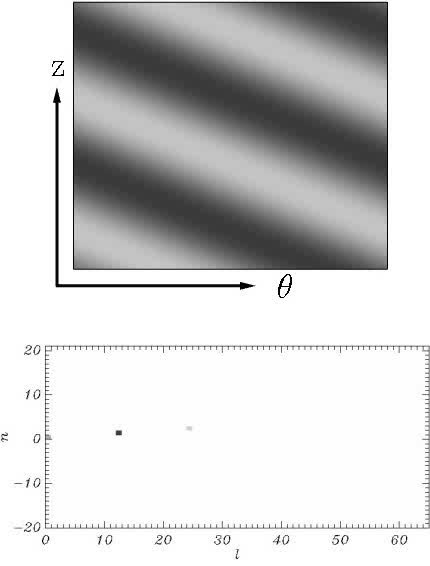
Movie 1. (a) Planar rendering of a gray-scale colormap of the azimuthal vorticity of the perturbation u at the outer cylinder r=ro, where black (white) corresponds to positive (negative) values. (b) Distribution of the kinetic modal energy decomposition, where black corresponds to the energy of the leading mode and white to a level seven orders of magnitude lower. The flow is a left-handed M1 spiral wave at A=79.6 and Re=246.32. Note that M1 is a rotating and traveling wave, precessing in the positive azimuthal direction while traveling in the positive axial direction. The spiral angle is about -23 degrees.
 |
Movie 2. Perspective view (parallel projection of the cylinder). The gray-scale colormap shows the intensity of azimuthal vorticity of the perturbation u for left and right handed M1 spiral waves respectively. The left-handed M1 is the same as in Movie 1. The right-handed M1 also precesses in the positive azimuthal direction, but travels in the negative axial direction. Its spiral angle is about 23 degrees. Note that the motion of the spiral patterns is modulated by the harmonic axial forcing. The parameter values are A=79.6 and Re=246.32.
 |
Movie 3. Same as Movie 2 but for M2 wavy spirals at A=79.6 and Re=247. The time-dependent inclination of the spirals and the waviness, associated to the fast wavy frequency, can be clearly observed in contrast to Movie 2.
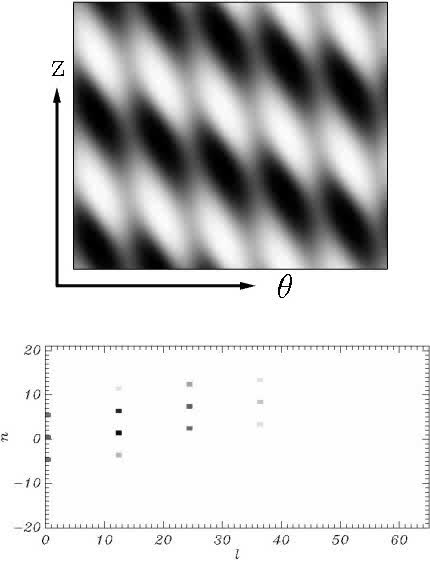 |
Movie 4. Sames as Movie 1. The flow is wavy spirals (M2) at A=79.6 and Re=247. Waviness is superposed now to the spirals which also feature a time-dependent angle. The modal kinetic energy is changed by the presence of the wavy mode (l,n)=(0,5).
 |
Movie 5. Sames as Movie 3 for secondary wavy spirals (M3) at A=79.6 and Re=249. The flow is very similar to the wavy spirals. However, the deffects on the wavy azimuthal wavenumber are visible in contrast to Movie 3.
 |
Movie 6. Sames as Movie 4. The flow is M3 at A=79.6 and Re=249. Deffects on the wavy azimuthal wave number can be clearly observed in M3 as opposite to M2 (compare with Movie 4). This can also be seen in the modal kinetic energies distribution featuring a broad-band of azimuthal wavenumbers.
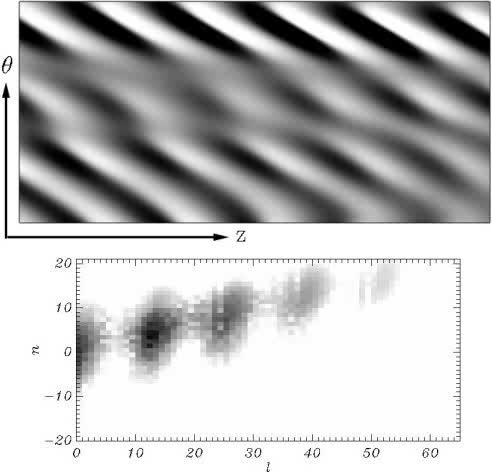 |
Movie 7. Sames as Movies 4 and 6. The flow is defective wavy spirals (M4) at A=79.6 and Re=250. M4 has lost all the symmetries and deffects on the axial and azimuthal wavenumbers can be clearly observed. The modal kinetic energy features a broad-band in both azimuthal and axial wavenumbers, illustrating the spatio-temporal complexity of the flow (compare to Movies 4 and 6).
 |
Movie 8. Same as Movies 3 and 5 for M4 defective wavy spirals at A=79.6 and Re=250. The flow is spatio-temporally complex, featuring defects in both the axial and aziumthal wavenumber (compare to Movies 3 and 5).