Interacting Stokes layers and wall modes in modulated rotating convection

A. Rubio, Juan M. Lopez and F. Marques

If a movie does not open, do: right click, Save Link as... and then choose to save it or to play it with your preferred movie player (mpv, vlc, ...)

Movie 1. Movie 2. Movie 3.

Movie 1. Wall-localized convection in Rayleigh-Bénard convection with constant rotation. In this Coriolis force dominated regime the onset of convection is to rotating waves of thermal plumes near the sidewall, the so-called wall modes of rotating convection. This solution has wave number m = 17 and becomes linearly stable at Ra = 4.23x104. The m = 17 wall mode loses stability to a mixed Küppers-Lortz/wall mode solution at about Ra=9.5x104, the convection threshold predicted by Chandrasekhar. This movie corresponds to figure 2 in the paper. Shown are isosurfaces of the temperature perturbation at Θ= +/- 0.05 for a solution with Ra=5x104, Ω0=625 & γ=4.

Movie 2. The m = 17 wall mode from movie 1 is subjected to a modulated rotation rate given by Ω(t) = Ω0(1+A sin(Ωmt)) (in the laboratory frame). Shown are isosurfaces of the temperature perturbation at Θ = +/-0.05 for Ra=5x104, Ω0=625, A=0.0075, ΩM=101.75 & γ=4.

Movie 3. Quenching of the m = 17 wall mode from movie 1 using a modulation amplitude slightly larger than that used in movie 2. Shown are isosurfaces of the temperature perturbation at Θ = +/- 0.05 for Ra=5x104, Ω0=625, A=0.01, ΩM=101.75 & γ=4. The three movies are shown in the rotating reference frame.


Movie 4.

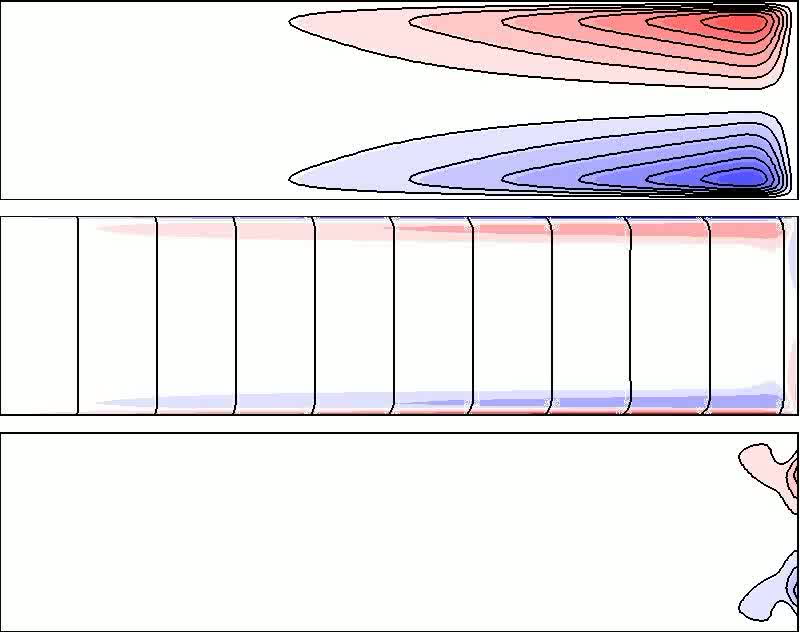Movie 4. The axisymmetric synchronous state of modulated Rayleigh-Bénard convection at Ra=4x104, Ω0=625, A=0.05, Ωm = 101.75 & γ=4. Here Ra < Rac and thermal convection is absent. However, the modulated rotation drives an alternating secondary flow by vortex line bending as the cylinder accelerates and decelerates. The top panel shows ten positive (red) and ten negative (blue) contours of the stream function Ψ ∈ [-1.5,1.5], in a meridional plane r ∈ [0,γ], z ∈ [-0.5,0.5]. The middle frame shows five positive (red) and five negative (blue) quadratically spaced color levels of the azimuthal vorticity ηz∈ [-1000,1000] and ten quadratically spaced contours of the vortex lines rv+r2Ω0 ∈[0,104]. The bottom frame shows ten positive (red) and ten negative (blue) contours of the thermal perturbation Θ ∈ [-0.12,0.12]. This movie corresponds to figure 5 in the paper.